Aerodynamic tools play an important role in understanding and obtaining solutions for some practical aerodynamic problems.
FLOW PAtterns
Fluid Mechanics can be visualized and interpreted by observing the motion of the flow and particles. When a particle of the fluid translates from one point to another, one can observe different patterns of motion (curves). You can learn to a great extent qualitatively and often quantitatively about the flow from these patterns.

The flow patterns of the particles to visualize the flow can be categorized as:
- Streamlines
- Pathlines
- Streaklines
Streamlines
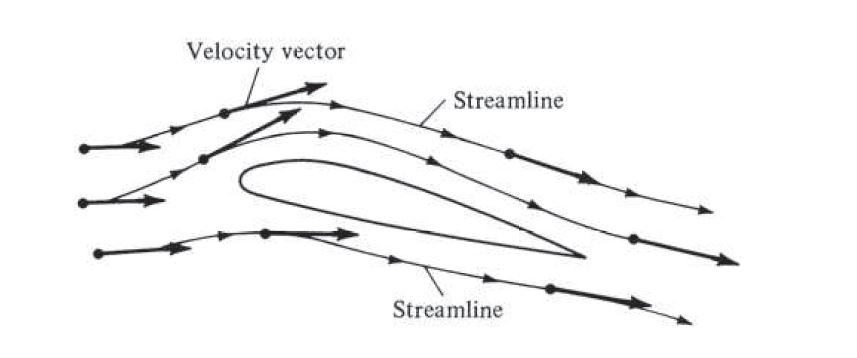
Streamlines can be defined as the curve whose tangent is in the direction of the local velocity vector at a point (Fig. 2). Streamlines are easier to calculate mathematically and are instantaneous lines. In unsteady flow, the pattern of the streamlines may vary at different times as the velocity vector may fluctuate with time in both magnitude and direction. In steady flow, the magnitude and direction of the velocity vector will not vary with time and will be fixed, so the streamline pattern won’t vary but will be the same throughout the flow. Streamline patterns are used as a common mathematical result for visualization purposes in fluid mechanics.
To express analytically the equation of a streamline at a certain instant of time, at any point P in the fluid, the velocity q must be parallel to the streamline element dl (Fig. 3). Therefore, on a streamline:
q × dl = 0 – Eq1

If the velocity vector is q = (u, v,w), then the vector equation (Eq 1) reduces to the following scalar equations:
w dy − v dz = 0
u dz − w dx = 0
v dx − u dy = 0
or in a differential equation form:
dx/u = dy/v = dz/w
Pathlines
Pathlines can be defined as a line or a curve describing the trajectory of the fluid particle. Pathlines are easy to generate experimentally. Pathlines can be obtained in the Lagrangian approach by an integration of the equations of dynamics for each fluid particle.

Consider an unsteady flow with a velocity field V and an infinitesimal fluid element A moving through the flow field. Now the element A passes through point 1 to another point (Fig 4). The path or the trajectory covered by the fluid element from one point to another is known as the pathline. The pathlines may vary for different fluid elements passing through the same point
Streaklines
Streaklines can be defined as the locus of particles that have earlier passed through a prescribed point. Streaklines are easy to generate experimentally. Streaklines can be constructed using the Lagrangian approach, by drawing a series of pathlines for fluid particles passing through a point in space and, at a particular instant in time, and then connecting the ends of these pathlines.
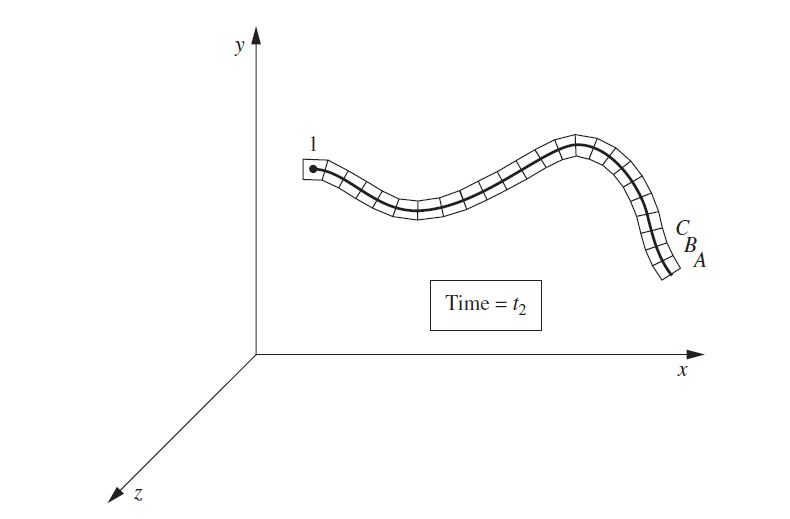
Consider all the individual particles that have passed through a point 1 over a time interval of t1- t2. Fluid element A has passed through point A at time t1, fluid element B is the next particle to pass through point 1 just behind element A. Now, the fluid element C passes through the same point 1 after element B (Fig 5). The line that connects all these fluid elements that have passed through point 1 over the time interval t1 -t2 is known as Streaklines.
Circulation
Circulation is an important fundamental aerodynamic tool that helps us to obtain solutions for some practical aerodynamic problems. Circulation plays a key role in the generation of lift in the inviscid framework.
By definition, circulation is the line integral of velocity around a closed curve in the flow. Consider an open surface S, (Fig. 6) with a closed curve C as its boundary. By using Stokes’s theorem the vorticity on the surface S can be related to the line integral around C. Let V and ds be the velocity and directed line segment, respectively, at a point on C.
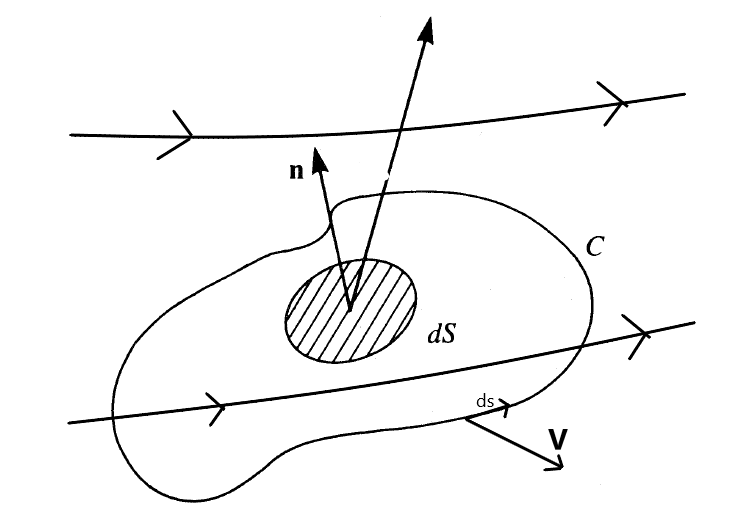
It is a kinematic property depending only on the velocity field and the choice of the curve C. In Aerodynamics, it is convenient to consider a positive circulation as clockwise. In inviscid flow, the only source for the generation of lift is through circulation only. If the circulation is finite then the lift will be finite.
The term circulation may not be misunderstood by considering the fluid elements moving around in circles within the flow field but it simply means that the line integral is finite.
Credits – Frank White, Katz & Plotkin, J.D Anderson.
*The information provided herein is, to the best of our knowledge and is only for informative purpose. If you have a news update or correction, let us know at -info@garudauniverse.com





Nicely summarized.
Informative!