When a fluid is moving from one location to another, the molecules experience mass diffusion, viscosity, and thermal conduction. We will discuss and distinguish between the viscous flow and inviscid flow.
Key points
Friction
Viscosity
Reynolds Number
Ideal/Real Flow
Pressure Distribution
Inviscid Flow

A flow is assumed to be inviscid when the viscosity is very low or almost negligible i.e there is no friction between the fluid layers then we assume the flow to be inviscid. There is also very limited or no mass diffusion and thermal conduction among the particles. Reynolds number approaches infinity because it is inversely proportional to the viscosity, which approaches zero for the inviscid flow. Navier-Stokes equation can further be simplified to the Euler equation since viscosity is zero or insignificant. Ideally, no real inviscid flow exists in nature but we use it to simplify the mathematical calculations for Mach Number below 0.3 as Bernoulli’s principle can then be applied, which seems to provide answers with enough accuracy.
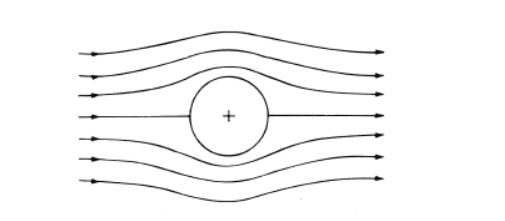
Shear stress acting across the body will be very low or equivalent to zero. There will be no net unbalanced forces acting on the body in the inviscid flow so no aerodynamic forces are produced in this flow. Therefore, lift and drag for inviscid flow are zero. The flow lines are symmetric and parallel to the flow of direction of streamlines. The pressure around the surface of the body is distributed symmetrically. The velocity at the surface of the body will not be equivalent to zero.
Viscous Flow
When the molecules move from one location to another, they transport their mass, momentum, and energy in the fluid and gives rise to mass diffusion, viscosity (friction), and thermal conduction. A flow where the viscous forces are present is known as the viscous flow. Friction forces are acting between the fluid layers. Reynolds number is finite for viscous flow. Practically, all the flows are viscous flow only, no matter how small may be the magnitude of the force but it is present.
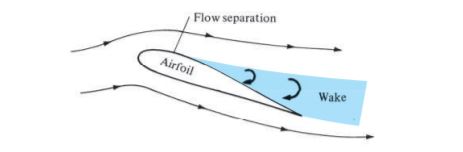
In viscous flow, the velocity at the surface of the body will be zero. Due to the presence of the viscosity, there will be a difference in the pressure distribution and also shear stress will vary along the body. Therefore, the net unbalanced forces will not be zero and the body will produce aerodynamic forces such as lift and drag. The pressure around the surface of the body will not be distributed symmetrically since velocity will change along the streamlines. Mass diffusion and thermal conduction will occur among the particles.
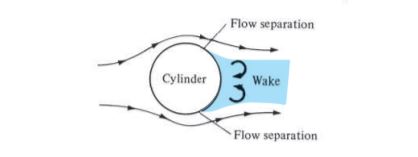
Credits – J D Anderson
* The information provided herein is, to the best of our knowledge and is only for informative purpose. If you have a news update or correction, let us know at -info@garudauniverse.com





Heу Тhere. I found your blog using msn. This is an extremely well ԝritten article.
I wіll be sure tо bߋokmark it and return to
read more of your useful information. Thanks for the post.
I’ll definitely rеturn.